Berechnung von Regressions-Polynomen

Für die Analyse von Prozessen ist der Zusammenhang zwischen Ein- und Ausgabeparametern oft wichtig. So auch bei einem Projekt, an dem wir gerade gearbeitet haben. Konkret ging es um die Auswertung von Mess- und Diagnosewerten, die von einer Reihe von externen Maschinen geliefert werden. Wir wollten die eher theoretischen Idealwerte und die während des Betriebs tatsächlich gemessenen Werte in Zusammenhang setzen, mit dem Ziel das Verhalten der Maschinen zu simulieren.

Dazu müssen zunächst Messungen durchgeführt werden, bei denen die Ausgabeparameter für verschiedene Kombinationen von Eingabeparametern bestimmt werden. Anhand dieser Messwerte können dann Funktion bestimmt werden, die diese Zusammenhänge annäherungsweise wiederspiegeln. Damit können dann Vorhersagen über die zu erwarteten Ausgabewerte für beliebige Eingaben treffen.

Eine verbreitete Methode für die Bestimmung einer solchen Funktion ist die Berechnung von Regression-Polynomen. Dabei wird der Zusammenhang zwischen den Eingabeparametern X=(x₁, … , x_n) und einem Ausgabeparameter (y) durch eine Funktion f(X) abgebildet, bei der die Wert für den Ausgabeparameter als gewichtete Summen aus Termen der Form term_i(X)=x₁^exp₁⋅x₂^exp₂⋅…⋅x_n^exp_n berechnet werden.

Viele Programme zur Datenanalyse bieten Funktionen zur Berechnung von Regressions-Polynomen. Oftmals sind diese aber auf Daten beschränkt, die aus Paaren von Ein- und Ausgabeparametern bestehen. Oder es werden maximal Polynome ersten Grades (Linien/Ebenen) als Terme unterstützt: in Microsoft Excel beispielsweise gibt es die Funktion RGP, die genutzt werden kann um Regressions- Linien/Ebenen zu berechnen.

In unserem Fall waren aber teilweise auch 3 Dimensionen beteiligt. Konkret hatten wir z.B. bei einem Kompressor Temperatur und Stromstärke als Eingabe- und den Druck als Ausgabewert.

Damit das Polynom die Zusammenhänge zwischen Ein- und Ausgabeparametern möglichst genau abbildet, müssen die Gewichte für die im Polynom enthaltenen Terme bestimmt werden, für die die Summe der quadratischen Abweichungen zwischen den gemessenen und berechneten Ausgabewerten für die gemessenen Eingabewerte minimal wird.

Dazu muss das Minimum der Funktion f(a₁,…,a_n)=∑[y_i-∑a_jterm_j(X_i)]² bestimmt werden, wobei a₁, …,a_n die zu bestimmenden Gewichte, y₁,…,y_m die Messwerte und X₁,…,X_m die Eingabewerte für die Messwerte sind. Diese Funktion wird minimal, wenn alle ihre partiellen Ableitungen null sind. Somit ergibt sich eine lineares Gleichungssystem mit einer Gleichung ∂f(a₁,…,a_n)/∂a_i=0 für jedes zu bestimmende Gewicht (a_i).

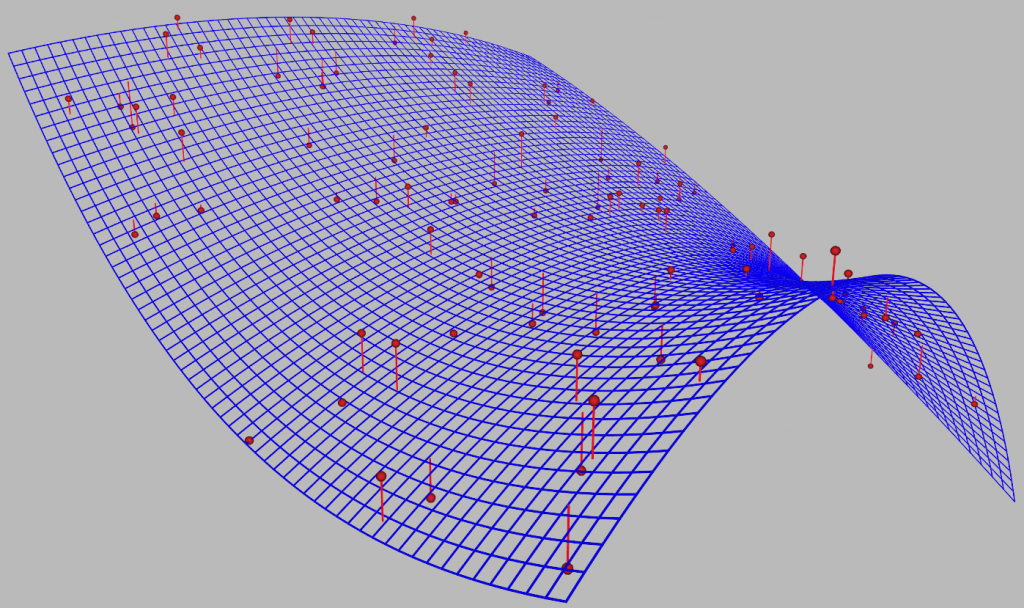
Für das Lösen von linearen Gleichungssystemen gibt es mehrere Algorithmen und für die meisten dieser Algorithmen gibt es Implementierungen für verschiedene Programmiersprachen. Die meisten dieser Algorithmen erwarten jedoch ein Gleichungssystem der Form Ma=y, daher muss das zu lösende Gleichungssystem in diese Form gebracht werden.

Für die Bestimmung der Gewichte a=(a₁,…,a_n) erhält man durch Umformen ein Gleichungssystem Ma=y mit y=(∑y_i⋅term₁(X_i), …, ∑y_i⋅term_n(X_i)) und einer Matrix M mit den Elementen M_u,v=∑term_u(X_i)⋅term_v(X_i).

Da die Berechnung von Regressions-Polynomen eine wichtige Funktionalität für die Analyse von Daten ist, haben wir diese Funktionalität auch in unsere VR-Datenanalyse- und Visualisierungs-Software FlaVR eingebaut. Das Beispiel aus dem Screenshot oben kann unter https://flavrapp.flavia-it.de/share/hhWvchtM eingesehen werden.